机器学习 - 强化学习示例
想象一下,你在教一只小狗学习坐下这个指令。你不会直接告诉它坐下这个单词是什么意思,而是通过奖励和惩罚来引导它。
- 当小狗偶然做出坐下的动作时,你立刻给它一块零食(奖励)。
- 当它做错时,你就不给零食(惩罚)。
经过多次尝试,小狗最终会明白坐下这个指令与获得零食之间的关联,从而学会这个技能。
强化学习 就是让计算机(或智能体)通过类似试错的方式,在与环境的互动中学习如何做出最优决策,以获得最大累积奖励的一种机器学习方法。
强化学习与我们之前学过的监督学习(有标准答案)和无监督学习(寻找数据内在结构)有本质区别。强化学习的核心是 智能体 与 环境 的持续交互。
核心概念解析
在深入代码之前,我们先来理解几个关键概念,它们就像游戏规则,定义了强化学习世界如何运转。
-
智能体:智能体就是我们的学习者或决策者。在上面的比喻中,它就是那只小狗。在程序中,它是一个算法,负责观察环境、做出动作并从结果中学习。
-
环境:环境是智能体所处的外部世界。它接收智能体的动作,并给出两个反馈:新的环境状态和本次动作带来的即时奖励。
-
状态:状态是环境在某一时刻的具体情况描述。例如,在一个走迷宫的游戏里,状态就是智能体当前所在的位置坐标。
-
动作:动作是智能体在某个状态下可以做出的选择。比如,在迷宫中,动作可以是向上、向下、向左、向右。
-
奖励:奖励是环境对智能体动作的直接评价信号,通常是一个数值。正奖励 表示鼓励,负奖励 表示惩罚。智能体的终极目标就是最大化从开始到结束所获得的 总奖励(累积奖励)。
-
策略:策略是智能体的行为准则,它定义了在每一个可能的状态下,应该选择哪个动作。学习的过程,本质上就是优化这个策略的过程。
为了更直观地理解这些概念如何协同工作,我们来看一下强化学习的基本交互流程:
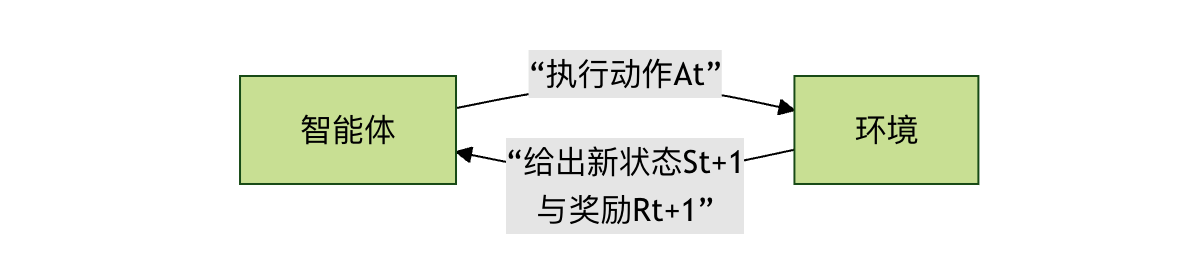
这个循环会一直持续,直到达到终止状态(如游戏通关或失败)。
经典问题:悬崖寻路
为了将理论付诸实践,我们将使用一个经典的强化学习示例环境:CliffWalking-v0(悬崖寻路)。它来自 gymnasium 库(原 OpenAI Gym 的维护分支)。
环境描述
- 场景:一个 4x12 的网格世界。
- 起点:左下角(坐标 [3, 0])。
- 终点:右下角(坐标 [3, 11])。
- 悬崖:最底部一排除了起点和终点的所有位置([3, 1] 到 [3, 10]),掉入悬崖会获得巨大惩罚并回到起点。
- 目标:智能体要从起点安全地走到终点,并避免掉下悬崖。
- 动作:上(0)、右(1)、下(2)、左(3)。
- 奖励:
- 每走一步普通网格:-1(鼓励用更少步数到达)
- 掉下悬崖:-100,并被送回起点
- 到达终点:0,并结束本次尝试
算法简介:Q-Learning
我们将使用 Q-Learning 算法来解决这个问题。它是一种 无模型 的强化学习算法,意味着智能体不需要预先知道环境的运作规则(如状态转移概率),它通过不断尝试来学习。
它的核心是一个名为 Q表 的表格。
- 行 代表所有可能的状态。
- 列 代表所有可能的动作。
- 单元格的值(Q值) 代表在某个状态下,采取某个动作的长期期望收益。
Q-Learning 的学习过程可以概括为以下几步,它展示了智能体如何通过一次经验来更新自己的知识(Q表):
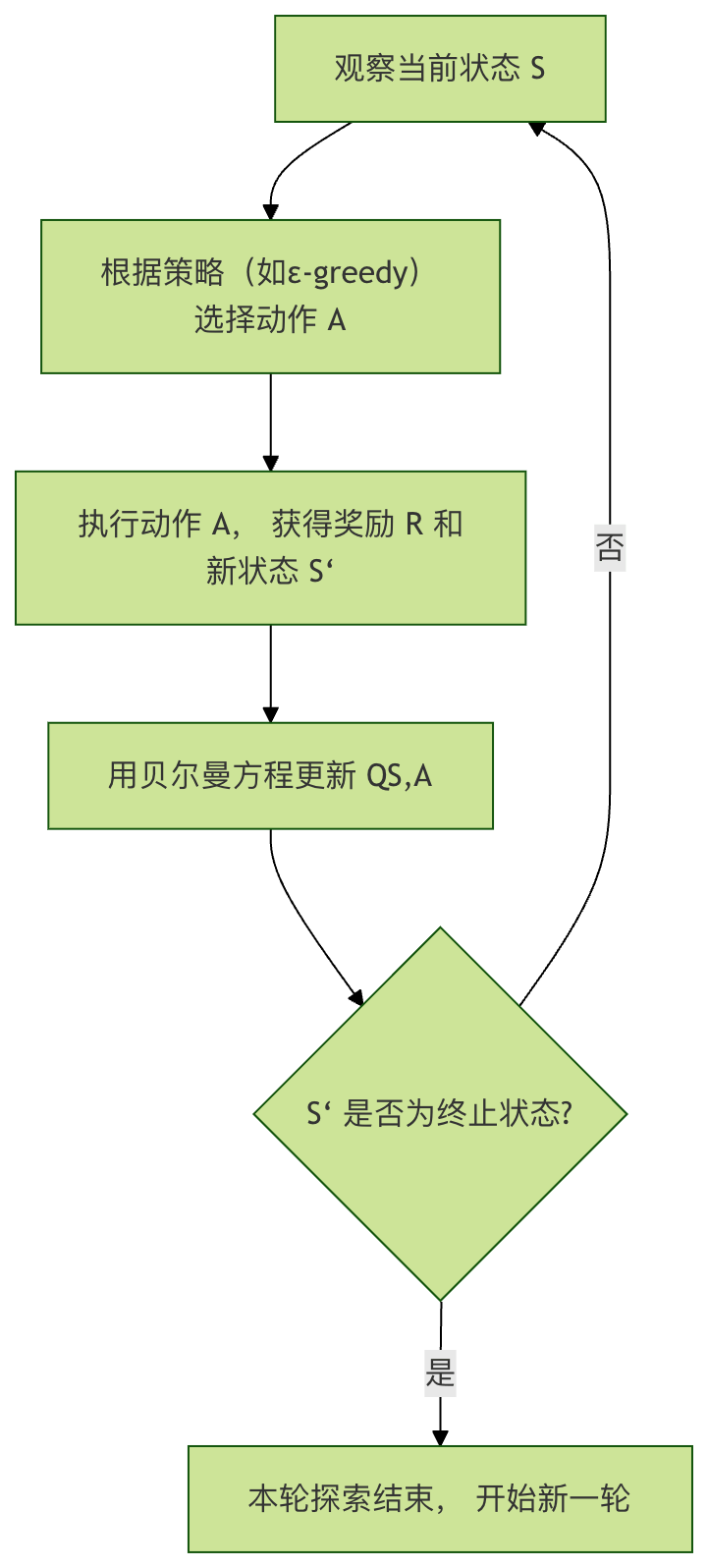
核心公式:贝尔曼方程
Q表更新的数学基础是贝尔曼方程,其更新公式如下:
\[ Q(S, A) \leftarrow Q(S, A) + \alpha [R + \gamma \max_{a} Q(S', a) - Q(S, A)] \]
让我们拆解这个公式中的每个部分:
| 符号 | 含义 | 类比解释 |
|---|---|---|
| \( Q(S, A) \) | 状态S下动作A原有的Q值 | 你之前对在十字路口直行这个决策的旧评分 |
| \(\alpha \) | 学习率 (0 < α ≤ 1) | 你有多相信这次的新经验。α=1表示完全用新经验覆盖旧认知;α=0.1表示新经验只轻微修正旧认知 |
| \(R \) | 执行动作A后获得的即时奖励 | 你直行后,发现道路通畅,获得了一个小的正反馈(+1) |
| \(\gamma \) | 折扣因子 (0 ≤ γ < 1) | 你对未来奖励的重视程度。γ=0表示只在乎眼前奖励;γ=0.9表示非常重视长远收益 |
| \(\max_{a} Q(S', a) \) | 在新状态S'下,所有可能动作中最大的Q值 | 到达新路口后,你评估左转、右转、直行哪个未来收益最高 |
| \(R + \gamma \max_{a} Q(S', a)\) | 目标Q值,代表对当前决策的新的、更优的估计 | 结合即时奖励和未来最佳收益,得出对在旧路口直行这个决策的新评分 |
| \(R + \gamma \max_{a} Q(S', a) - Q(S, A)\) | 时序差分误差,新老认知的差距 | 新评分与旧评分的差距,这个差距驱动学习 |
简单来说,这个公式让智能体用 即时奖励 + 对未来最优估计的折扣 来不断修正自己对当前决策价值的判断。
实战:编写Q-Learning智能体
现在,让我们用代码实现一个解决悬崖寻路问题的Q-Learning智能体。
步骤1:安装与导入库
首先,确保你已安装必要的库。在终端或命令行中运行:
实例
然后,在Python文件中导入它们:
实例
import numpy as np
import random
步骤2:初始化环境和Q表
实例
env = gym.make("CliffWalking-v0", render_mode="human") # render_mode="human" 用于可视化
# 2. 获取环境信息
n_states = env.observation_space.n # 状态总数 (4*12=48)
n_actions = env.action_space.n # 动作总数 (4个方向)
# 3. 初始化Q表, 形状为 [状态数, 动作数], 初始值全为0
Q_table = np.zeros((n_states, n_actions))
print(f"环境状态数: {n_states}, 动作数: {n_actions}")
print(f"Q表形状: {Q_table.shape}")
步骤3:设置超参数
超参数是控制算法行为的旋钮,需要根据问题调整。
实例
alpha = 0.1 # 学习率:新信息的影响程度
gamma = 0.99 # 折扣因子:未来奖励的重要性
epsilon = 0.1 # 探索率:以多大概率进行随机探索(而非选择已知最优)
num_episodes = 500 # 训练轮数(智能体玩游戏的次数)
步骤4:实现ε-greedy策略
这是智能体做决策的核心策略,它平衡了 探索 和 利用。
- 探索:随机选择动作,以发现可能更好的策略。
- 利用:选择当前Q表认为最优的动作,以获取最大收益。
实例
"""
根据ε-greedy策略选择动作。
参数:
state: 当前状态
Q_table: Q值表
epsilon: 探索概率
返回:
action: 选择的动作 (0, 1, 2, 3)
"""
# 生成一个0-1之间的随机数
if random.uniform(0, 1) < epsilon:
# 探索:随机选择一个动作
action = env.action_space.sample()
else:
# 利用:选择当前状态下Q值最大的动作
# np.argmax 返回最大值的索引,即最优动作
action = np.argmax(Q_table[state])
return action
步骤5:核心训练循环
这是算法学习的主要过程。
实例
reward_history = []
for episode in range(num_episodes):
# 重置环境,获取初始状态
state, _ = env.reset()
total_reward = 0 # 本轮累积奖励
terminated = False # 是否到达终止状态(终点/悬崖)
truncated = False # 是否因步数超限而终止(本环境一般不会)
# 本轮交互循环,直到游戏结束
while not (terminated or truncated):
# 1. 选择动作
action = choose_action(state, Q_table, epsilon)
# 2. 执行动作,获取环境反馈
next_state, reward, terminated, truncated, _ = env.step(action)
# 3. 更新Q表 (Q-Learning 核心更新公式)
# 获取当前Q值
current_q = Q_table[state, action]
# 计算目标Q值:即时奖励 + 未来最大Q值的折扣
# 注意:如果下一状态是终止状态,则没有未来Q值
if terminated:
target_q = reward
else:
target_q = reward + gamma * np.max(Q_table[next_state])
# 应用贝尔曼方程更新Q值
Q_table[state, action] = current_q + alpha * (target_q - current_q)
# 4. 转移到下一个状态,并累积奖励
state = next_state
total_reward += reward
# 记录本轮总奖励
reward_history.append(total_reward)
# 每100轮打印一次进度
if (episode + 1) % 100 == 0:
avg_reward = np.mean(reward_history[-100:]) # 最近100轮的平均奖励
print(f"轮次 {episode + 1}, 最近100轮平均奖励: {avg_reward:.2f}")
# 训练结束,关闭环境
env.close()
步骤6:测试训练好的智能体
训练完成后,我们关闭探索,让智能体纯粹利用学到的知识(Q表)来走一遍,看看它的表现。
实例
# 创建新的测试环境(可以不加render_mode,或改为"human"观看)
test_env = gym.make("CliffWalking-v0", render_mode="human")
state, _ = test_env.reset()
test_terminated = False
test_truncated = False
step_count = 0
while not (test_terminated or test_truncated):
# 测试时,我们设置 epsilon=0, 即完全利用,不探索
action = choose_action(state, Q_table, epsilon=0)
state, reward, test_terminated, test_truncated, _ = test_env.step(action)
step_count += 1
print(f"步骤 {step_count}: 状态 {state}, 动作 {action}, 奖励 {reward}")
print(f"测试完成!总步数: {step_count}, 总奖励: {reward} (到达终点奖励为0)")
test_env.close()
运行结果与分析
完整代码:
实例
import numpy as np
import random
# =========================
# 1. 创建环境
# =========================
env = gym.make("CliffWalking-v0", render_mode="human")
# =========================
# 2. 获取环境信息
# =========================
n_states = env.observation_space.n
n_actions = env.action_space.n
# =========================
# 3. 初始化 Q 表
# =========================
Q_table = np.zeros((n_states, n_actions))
print(f"环境状态数: {n_states}")
print(f"动作数: {n_actions}")
print(f"Q表形状: {Q_table.shape}")
# =========================
# 4. 设置超参数
# =========================
alpha = 0.1
gamma = 0.99
epsilon = 0.1
num_episodes = 500
# =========================
# 5. ε-greedy 策略
# =========================
def choose_action(state, Q_table, epsilon):
if random.uniform(0, 1) < epsilon:
return env.action_space.sample()
return np.argmax(Q_table[state])
# =========================
# 6. 训练循环
# =========================
reward_history = []
for episode in range(num_episodes):
state, _ = env.reset()
total_reward = 0
terminated = False
truncated = False
while not (terminated or truncated):
action = choose_action(state, Q_table, epsilon)
next_state, reward, terminated, truncated, _ = env.step(action)
current_q = Q_table[state, action]
if terminated:
target_q = reward
else:
target_q = reward + gamma * np.max(Q_table[next_state])
Q_table[state, action] = current_q + alpha * (target_q - current_q)
state = next_state
total_reward += reward
reward_history.append(total_reward)
if (episode + 1) % 100 == 0:
avg_reward = np.mean(reward_history[-100:])
print(f"轮次 {episode + 1},最近100轮平均奖励: {avg_reward:.2f}")
env.close()
# =========================
# 7. 测试训练结果
# =========================
print("\n=== 开始测试 ===")
test_env = gym.make("CliffWalking-v0", render_mode="human")
state, _ = test_env.reset()
terminated = False
truncated = False
step_count = 0
total_reward = 0
while not (terminated or truncated):
action = choose_action(state, Q_table, epsilon=0)
state, reward, terminated, truncated, _ = test_env.step(action)
step_count += 1
total_reward += reward
print(f"步骤 {step_count}: 状态 {state}, 动作 {action}, 奖励 {reward}")
print(f"测试完成,总步数: {step_count},总奖励: {total_reward}")
test_env.close()
运行上述完整代码后,你将看到两个非常直观的现象:训练阶段的奖励变化,以及测试阶段智能体的实际行动路径。
1. 训练阶段:奖励逐步提升
在训练过程中,控制台会每 100 轮输出一次最近 100 轮的平均奖励。例如:
轮次 100, 最近100轮平均奖励: -120.45 轮次 200, 最近100轮平均奖励: -65.32 轮次 300, 最近100轮平均奖励: -32.18 轮次 400, 最近100轮平均奖励: -18.06 轮次 500, 最近100轮平均奖励: -13.94
你会发现一个明显趋势:平均奖励在不断上升(负值绝对值变小)。
这说明什么?
- 在训练初期,智能体频繁掉入悬崖,受到大量
-100的惩罚。 - 随着训练进行,Q 表逐渐学习到"哪些路径危险、哪些路径安全"。
- 智能体开始主动绕开悬崖,选择一条虽然更长、但惩罚更小的安全路线。
奖励的提升,本质上反映了策略质量的提升。
2. 测试阶段:智能体的行为表现
在测试阶段,我们将 epsilon 设置为 0,意味着:
- 不再进行任何随机探索
- 完全按照 Q 表中学到的最优策略行动
如果你开启了 render_mode="human",会看到一个非常典型的行为:
- 智能体从起点出发
- 沿着悬崖上方一格的位置水平移动
- 在接近终点时再向下移动,安全抵达终点
这正是 CliffWalking 环境中被认为的最优策略:
- 不是最短路径(贴着悬崖)
- 而是期望惩罚最小的路径
这体现了强化学习的一个核心特征:它追求的是长期累计回报,而不是短期最优。
3. 为什么学到的是绕路,而不是冒险直走?
这是一个非常重要、也非常经典的问题。
从人类直觉来看,贴着悬崖走是最短路径,但对智能体来说:
- 一旦走错一步,立刻获得
-100的巨大惩罚 - 相比之下,多走几步只会多几个
-1
在贝尔曼方程的累计效应下:
稳定的小损失 < 偶发的大灾难
因此,Q-Learning 会自然收敛到一条更保守、但整体期望回报更高的策略。
常见问题与参数影响
1. 学习率 α 过大或过小会发生什么?
- α 过大:学习过程震荡,策略不稳定,容易反复推翻已有经验
- α 过小:学习非常慢,需要大量轮次才能收敛
在这个示例中,0.1 是一个相对稳妥的选择。
2. 折扣因子 γ 的直观含义
γ → 0:智能体只关心眼前奖励,容易变得短视γ → 1:智能体非常重视长期后果,更像有远见的规划者
在悬崖寻路问题中,较大的 γ 能帮助智能体意识到现在多走一步,是为了未来避免更大损失。
3. ε 的作用本质
ε 决定了智能体的性格:
- ε 大 → 爱冒险,探索多
- ε 小 → 保守,更多利用已有经验
在真实项目中,通常会使用 ε 衰减策略:
- 前期多探索
- 后期逐渐收敛到稳定策略
本示例的局限与扩展方向
虽然 Q-Learning 非常经典,但它也有明显限制:
- Q 表大小随状态空间线性增长
- 无法直接处理连续状态(如真实物理世界)
- 在复杂环境中收敛速度慢
这也是为什么在更复杂问题中,我们会引入:
- Deep Q-Network(DQN)
- Policy Gradient
- Actor-Critic
它们用神经网络替代 Q 表,使强化学习能够应用到游戏、机器人控制、自动驾驶等真实场景。
总结
通过这个完整的强化学习示例,你已经:
- 理解了强化学习与监督 / 无监督学习的根本区别
- 掌握了智能体、环境、状态、动作、奖励、策略的完整闭环
- 亲手实现了一个可运行、可观察、可收敛的 Q-Learning 智能体
- 理解了最大化长期回报这一强化学习的核心思想

点我分享笔记