机器学习 - PCA 可视化案例
想象一下,你正在整理一个塞满各种物品的杂乱房间,为了更清晰地了解房间的布局,你可能会从不同角度(比如正面、侧面、俯视)给它拍几张照片。
主成分分析(Principal Component Analysis,简称 PCA) 在机器学习中所做的事情与此类似。
PCA 是一种强大的数据降维和可视化工具。当我们的数据包含成百上千个特征(维度)时,这些数据就像身处一个超高维度的空间中,人类无法直观理解。
PCA 可以帮助我们找到数据中最重要的视角(即主成分),将数据投影到最重要的两三个维度上,从而让我们能够用二维或三维散点图来观察高维数据的结构和分布。
简单来说,PCA的目标是:
- 降维:用更少的特征来代表原始数据,减少计算量和存储空间,同时去除噪声。
- 可视化:将高维数据降至2维或3维,以便于我们直观地观察数据点之间的关系(如聚类、分离情况)。
PCA 核心原理与工作流程
PCA 的核心思想是寻找数据方差最大的方向。
方差越大,意味着数据在这个方向上的投影点越分散,所包含的信息量也就越多。
第一个找到的方向就是第一主成分(PC1),第二个与 PC1 正交且方差次大的方向是第二主成分(PC2),以此类推。
PCA 工作流程图
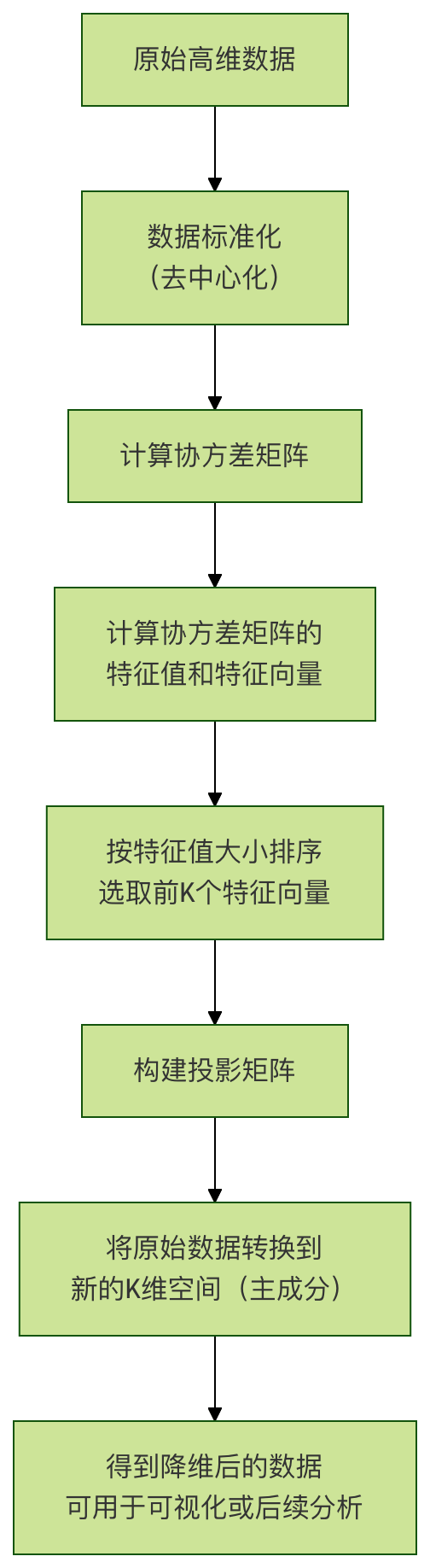
流程关键步骤说明:
标准化:让每个特征的平均值为 0,标准差为 1,确保所有特征在计算时具有同等重要性。
协方差矩阵:计算特征之间的相关性。PCA 通过分析这个矩阵来找到数据变化的主要方向。
特征值与特征向量:
- 特征向量:就是我们要找的主成分方向。
- 特征值:对应特征向量方向上的数据方差大小。特征值越大,该主成分越重要。
选择主成分:我们将特征值从大到小排序,选择前 K 个最大的特征值对应的特征向量。K 就是我们想要降维到的目标维度(例如,对于可视化,K=2 或 3)。
数据转换:用选出的 K 个特征向量组成一个投影矩阵,将原始数据点乘这个矩阵,就得到了在 K 个新主成分上的坐标,即降维后的数据。
实战案例:鸢尾花数据集的可视化
我们将使用经典的鸢尾花(Iris)数据集来演示PCA。这个数据集包含150个样本,每个样本有4个特征(萼片长度、萼片宽度、花瓣长度、花瓣宽度),并属于3个不同的品种。
我们的目标是:将这 4 维的数据用 PCA 降到 2 维,并在二维平面上画出来,观察不同品种的花是否能被区分开。
环境准备与数据加载
首先,确保你安装了必要的Python库:scikit-learn, matplotlib, numpy,pandas。
实例
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# 设置中文字体和图表样式(可选)
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data # 特征数据,形状为 (150, 4)
y = iris.target # 目标标签(品种),形状为 (150,)
target_names = iris.target_names # 品种名称:['setosa', 'versicolor', 'virginica']
print(f"数据集形状: {X.shape}")
print(f"特征名称: {iris.feature_names}")
print(f"目标类别: {target_names}")
输出:
数据集形状: (150, 4) 特征名称: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] 目标类别: ['setosa' 'versicolor' 'virginica']
数据标准化
在应用 PCA 之前,对数据进行标准化是至关重要的一步。
因为 PCA 对特征的尺度非常敏感,如果一个特征的数值范围(例如花瓣长度以厘米计,数值在 1-10 之间)远大于另一个特征(例如萼片宽度以毫米计,数值在 0.1-1 之间),那么数值范围大的特征会主导主成分的方向,这通常不是我们想要的。
实例
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
print("标准化后,前5个样本的数据:")
print(X_scaled[:5])
应用 PCA 进行降维
我们使用 scikit-learn 的 PCA 类,它可以轻松完成所有数学计算。
实例
pca = PCA(n_components=2)
# 在标准化后的数据上拟合PCA模型,并进行数据转换
X_pca = pca.fit_transform(X_scaled)
print(f"降维后的数据形状: {X_pca.shape}")
print(f"前5个样本在PC1和PC2上的坐标:\n{X_pca[:5]}")
# 查看各主成分的方差解释率
print(f"主成分方差解释率: {pca.explained_variance_ratio_}")
print(f"前两个主成分累计方差解释率: {sum(pca.explained_variance_ratio_):.4f}")
代码解析:
n_components=2:指定我们要将数据降至 2 维。
fit_transform(X_scaled):该方法一次性完成两件事:
fit:根据输入数据X_scaled计算 PCA 所需的参数(如主成分方向)。transform:使用计算好的参数,将数据X_scaled转换到新的二维空间。
explained_variance_ratio_:这是一个非常重要的属性。它告诉我们每个主成分捕获的原始数据方差的比例。例如,如果输出是 [0.73, 0.23],意味着PC1保留了原始数据73%的信息,PC2保留了23%的信息,两者加起来保留了96%的信息。这帮助我们评估降维后的信息损失。
可视化结果
现在,我们有了二维数据 X_pca,可以轻松地用散点图将其可视化。
实例
plt.figure(figsize=(8, 6))
# 为每个品种设置不同的颜色和标记
colors = ['navy', 'turquoise', 'darkorange']
lw = 2 # 线宽
# 遍历三个品种,分别绘制
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
plt.scatter(X_pca[y == i, 0], # 选择属于当前品种i的样本的PC1坐标
X_pca[y == i, 1], # 选择属于当前品种i的样本的PC2坐标
color=color, alpha=0.8, lw=lw,
label=target_name)
# 添加图表标题和坐标轴标签
plt.title('鸢尾花数据集的PCA二维可视化')
plt.xlabel(f'第一主成分 (PC1) - 方差解释率: {pca.explained_variance_ratio_[0]:.2%}')
plt.ylabel(f'第二主成分 (PC2) - 方差解释率: {pca.explained_variance_ratio_[1]:.2%}')
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.grid(True, linestyle='--', alpha=0.6)
# 显示图表
plt.tight_layout()
plt.show()
可视化结果解读: 运行上述代码后,你会得到一张二维散点图。
- X轴(PC1):代表了原始4个特征中方差最大的方向,是区分数据最重要的维度。从图中可以看出,它很好地将 Setosa(山鸢尾) 品种与其他两个品种分离开。
- Y轴(PC2):代表了与PC1正交且方差次大的方向,提供了额外的区分信息。它帮助进一步区分 Versicolor(杂色鸢尾) 和 Virginica(维吉尼亚鸢尾),尽管两者有一些重叠。
- 结论:通过PCA,我们成功将4维数据投影到2维平面,并清晰地观察到三个品种的聚类情况。Setosa完全分离,而Versicolor和Virginica在二维投影上存在部分重叠,这说明仅用前两个主成分(保留了约95%的信息)还不足以完美区分后两个品种,但它们的主要分布趋势已经非常明显。
深入探索与思考
如何选择主成分的数量(K值)?
在实际项目中,我们可能不知道应该降到几维。一个常用的方法是绘制 碎石图(Scree Plot),它展示了每个主成分的方差解释率。
实例
pca_full = PCA()
pca_full.fit(X_scaled)
# 绘制碎石图
plt.figure(figsize=(8, 5))
plt.plot(range(1, len(pca_full.explained_variance_ratio_) + 1),
pca_full.explained_variance_ratio_, 'o-', linewidth=2)
plt.title('PCA方差解释率碎石图')
plt.xlabel('主成分序号')
plt.ylabel('方差解释率')
plt.grid(True, linestyle='--', alpha=0.6)
plt.xticks(range(1, len(pca_full.explained_variance_ratio_) + 1))
plt.tight_layout()
plt.show()
# 绘制累计方差解释率图
plt.figure(figsize=(8, 5))
plt.plot(range(1, len(pca_full.explained_variance_ratio_) + 1),
np.cumsum(pca_full.explained_variance_ratio_), 's-', linewidth=2, color='red')
plt.title('PCA累计方差解释率')
plt.xlabel('主成分数量')
plt.ylabel('累计方差解释率')
plt.axhline(y=0.95, color='gray', linestyle='--', label='95% 阈值') # 常用阈值
plt.legend()
plt.grid(True, linestyle='--', alpha=0.6)
plt.xticks(range(1, len(pca_full.explained_variance_ratio_) + 1))
plt.tight_layout()
plt.show()
如何选择 K 值?
- 看拐点:在碎石图中,寻找方差解释率下降趋势突然变缓的点(即肘部),其后的主成分贡献较小。
- 设定阈值:在累计方差图中,选择能使累计解释率达到一个满意阈值(如 95% 或 99%)的最小K值。从鸢尾花数据的累计图可以看出,前两个主成分已能解释超过 95% 的方差,因此 K=2 是一个很好的选择。
理解主成分的含义
我们还可以查看主成分的载荷(Loadings),即每个原始特征对主成分的贡献权重,这有助于解释主成分的实际意义。
实例
pca_components = pca.components_ # 形状为 (2, 4)
# 用DataFrame展示,更清晰
df_components = pd.DataFrame(pca_components,
columns=iris.feature_names,
index=['PC1', 'PC2'])
print("主成分载荷矩阵(特征向量):")
print(df_components)
# 可以用热力图可视化
import seaborn as sns
plt.figure(figsize=(8, 4))
sns.heatmap(df_components, annot=True, cmap='RdBu_r', center=0)
plt.title('主成分载荷热力图')
plt.tight_layout()
plt.show()
解读载荷矩阵:
- 对于 PC1,如果花瓣长度和花瓣宽度有较大的正权重,而萼片宽度有较大的负权重,那么 PC1 可能主要代表了花瓣大小与萼片宽度的对比这个综合特征。
- 对于 PC2,权重模式不同,它可能代表了另一种特征组合。通过分析这些权重,我们可以为抽象的主成分赋予一些实际的生物学或业务含义。
总结与实践练习
关键要点总结
- PCA 是什么:一种无监督的线性降维方法,通过寻找数据方差最大的正交方向(主成分)来重新表述数据。
- 核心步骤:标准化 -> 计算协方差矩阵 -> 计算特征值与特征向量 -> 选择主成分 -> 数据投影。
- 重要概念:
- 主成分:新的、不相关的特征轴。
- 方差解释率:衡量每个主成分重要性的指标。
- 载荷:连接原始特征与主成分的桥梁,用于解释主成分的意义。
- 主要应用:数据可视化、去除噪声和冗余、作为其他模型(如分类、回归)的预处理步骤以加速训练。
动手练习
为了巩固知识,请尝试完成以下练习:
练习1:探索不同数据集
尝试对 scikit-learn 中的其他数据集(如 digits 手写数字数据集或 wine 葡萄酒数据集)进行 PCA 可视化。观察降维后的图像是否还能保留不同类别之间的区分度。
实例
from sklearn.datasets import load_wine
wine = load_wine()
# ... 重复PCA流程
练习2:三维可视化
将鸢尾花数据降至3维,并使用 mpl_toolkits.mplot3d 库进行三维散点图绘制。看看增加一个维度后,Versicolor和Virginica的重叠是否减少。
实例
pca3 = PCA(n_components=3)
X_pca3 = pca3.fit_transform(X_scaled)
# ... 创建3D图形进行绘制

点我分享笔记